
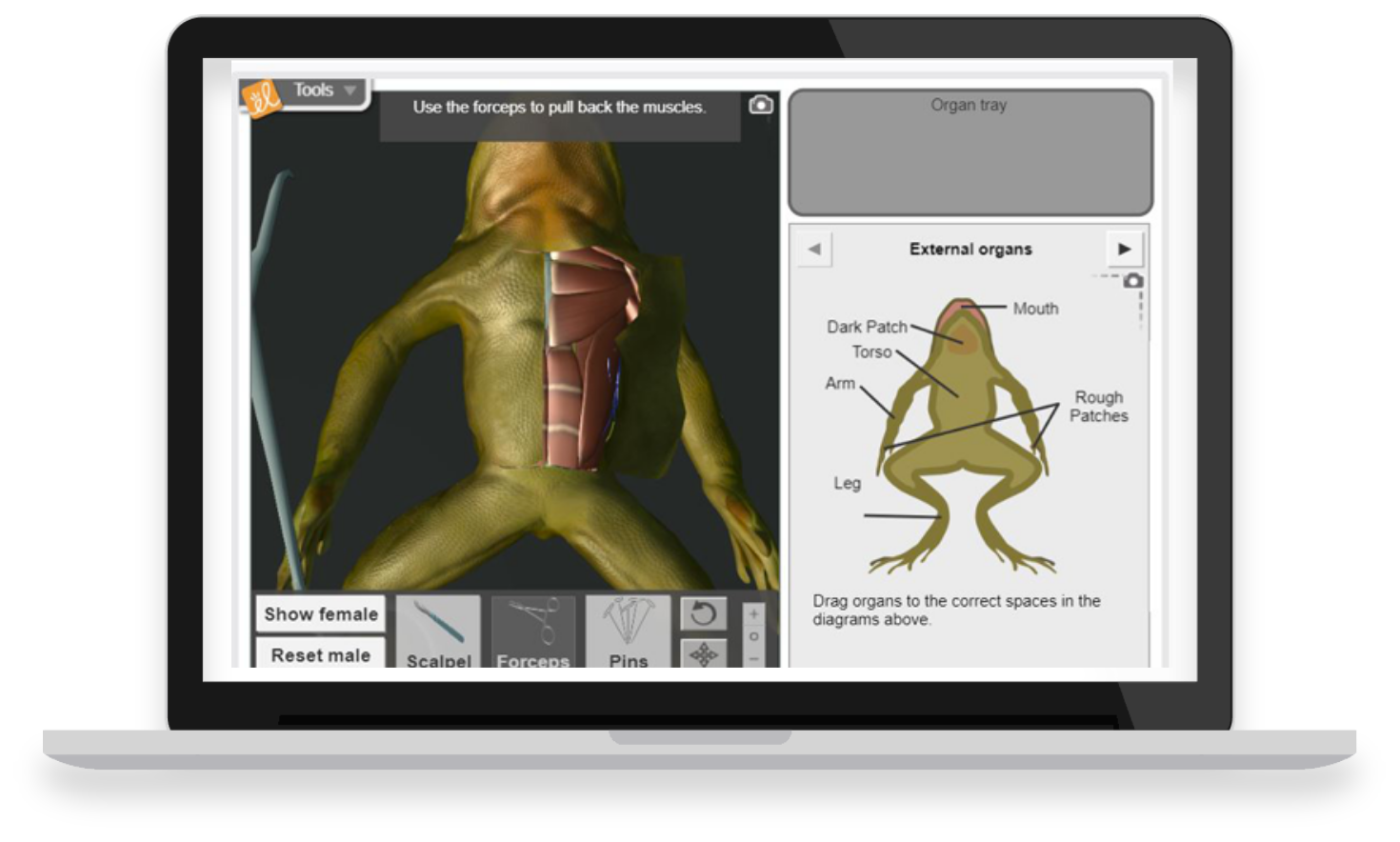
Meet Gizmos
The world's largest library of math and science simulations.
Sign Up for Free Find a Gizmo

Build inquiry, understanding, and a love of math and science.
With over 450 virtual, interactive STEM simulations all aligned to the latest standards, Gizmos help educators bring powerful new learning experiences to grade 3-12 classrooms.
Learn More about Gizmos Sign Up for FreeHoneybee Hive
Happy Earth Day! A great way to celebrate Earth Day (and spring) is with the Honeybee Hive Gizmo. This Gizmo celebrates the tiny workers who help keep the whole planet alive by pollinating plants.
...


Honeybee Hive
Happy Earth Day! A great way to celebrate Earth Day (and spring) is with the Honeybee Hive Gizmo. This Gizmo celebrates the tiny workers who help keep the whole planet alive by pollinating plants.
The Gizmo highlights the pioneering research of the Austrian zoologist Karl von Frisch (1886-1982). Using innovative techniques, Frisch determined that honeybees see in color, navigate and tell time using the Sun, and, incredibly, use a special “waggle dance” to communicate the location of food sources.
In the Gizmo, students get to design their own waggle dances and play the role of a forager bee. They locate flower beds in the landscape outside the hive and then create waggle dances to direct other foragers to those locations. By finding food sources and effectively communicating their location, students can keep the hive alive and growing.

Bring science to life with real-life STEM cases.
Gizmos STEM Cases put students in the roles of professionals tasked with solving real-world STEM problems — just like real scientists.
Learn More about STEM Cases Find a STEM Case

Research
Leverage research-proven teaching tools.
Independent research studies show how Gizmos interactive simulations power effective math and science instruction and impact student achievement.
See Our StudiesProfessional Development
Prepare teachers for even greater success.
When teachers effectively integrate Gizmos into instruction they can take learning to new levels. Learn how our support helps educators be their best.
Explore Our ServicesResources
Make the most of your implementation.
Get insights, ideas, inspiration and more. We’re here to help you use Gizmos in the classroom—whether you’re just getting started or ready to go deeper.
Browse Our Resources
Everybody's Talking About Gizmos
Hello, Ms. D. I apologize about emailing you during the weekend, but I couldn’t wait to tell you. Gizmos is so much fun, and I absolutely love it. I actually learn something and I like the fact that it is interactive. Thank you so much for making us do Gizmos.
- Gizmos Student, American International School, Abu DhabiI really love Gizmos as they help students grasp difficult concepts that can’t always be seen. They make abstract ideas come to life.
- Gizmos Teacher, Foothills School Division, Alberta, CanadaI’m really a strong proponent of Gizmos in science because I have seen firsthand what it does in terms of engaging kids in labs. Gizmos really allow students to go deeper in terms of problem solving and critical thinking.
- Gizmos Assistant Superintendent, Miami-Dade Public Schools, FLGizmos STEM Cases improve students’ content knowledge and critical thinking ability. The kids are putting more thought into things and they’re asking better questions.
- Gizmos Director of Science, Gwinnett County Public Schools, GAGizmos STEM Cases is the most engaging program that I’ve ever seen! High-quality graphics and real-world stories make them more thought-provoking than traditional teaching materials. Students become more personally invested in the lessons and feel a sense of accomplishment [when doing them].
- Gizmos Director of Science, Walker School, GA
Gizmos have earned every major edtech award!





Ready. Set. Gizmo! Create a free Gizmos trial account and get 45 days unlimited access to the entire Gizmos library.